编译原理作业3

Exercise 3.1

Give the recognized tokens of the following program in Pascal.

function max(i, j: integer): integer;
{return the maximum of integers i and j}
begin
	if i > j then max := i else max := j
end;

如果忽略注释，生成的token如下：

<Reserved words, function>

<Identifiers, max>

<Punctuation, (>

<Identifiers, i>

<Punctuation, ,>

<Identifiers, j>

<Punctuation, :>

<Reserved words, integer>

<Punctuation, )>

<Punctuation, :>

<Reserved words, integer>

<Punctuation, ;>

<Reserved words, begin>

<Reserved words, if>

<Identifiers, i>

<Operators, > >

<Identifiers, j>

<Reserved words, then>

<Identifiers, max>

<Operators, := >

<Identifiers, i>

<Reserved words, else>

<Identifiers, max>

<Operators, := >

<Identifiers, j>

<Reserved words, end>

Exercise 3.2

Describe the languages denoted by the following regular expressions:

• $a (a | b)* a $

• $a^* b \ a^* b\ a^* b \ a^* $

第一个式子表示由a和b组成且以a开头和a结尾的串

第二个式子表示由a和b组成且只包含3个b的串

Exercise 3.3

• Most Languages are case sensitive, so keywords can be written only one way, and the regular expressions describing their lexemes are very simple.

• However, some languages, like Pascal and SQL, are case insensitive. For example, the SQL keyword SELECT can also be written select, Select, or sELEcT.

• Show how to write a regular expression for a keyword in a case insensitive language. Illustrate your idea by writing the expression for SELECT in SQL.

表达式如下：

select -> (S|s)(E|e)(L|l)(E|e)(C|c)(T|t)

Exercise 3.4

Given the following regular expression :
$$ 1^*(0 \ |\ 01)^*$$
(1) Transform it to an equivalent finite automaton.

如图：

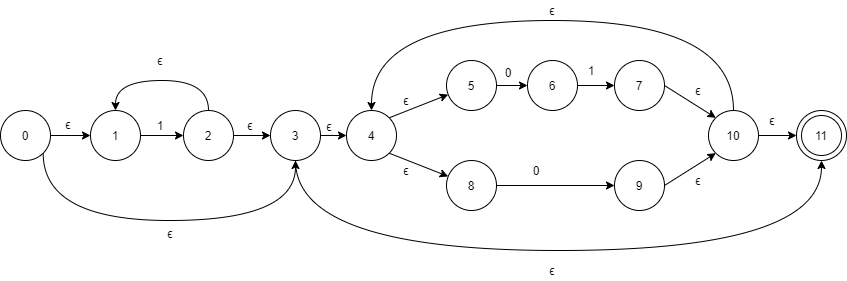
(2) Construct an equivalent DFA for the result of exercise (1).

$$\epsilon -closure({0}) = {0,1,3,4,5,8,\textbf{11}} = A
\
\delta(A,0) = {6,9}
\
\epsilon -closure( {6,9}) = {6,9,10,\textbf{11},4,5,8} = B
\
\delta(A,1) = {2}
\
\epsilon -closure( {2}) = {2,1,3,4,5,8,\textbf{11}} = C
\
\delta(B,0) = {6,9}
\
\epsilon -closure( {6,9}) = B
\
\delta(B,1) = {7}
\
\epsilon -closure( {7}) = {10,\textbf{11},4,5,8} = D
\
\delta(C,0) ={6,9}
\
\epsilon -closure( {6,9}) = B
\
\delta(C,1) = {2}
\
\epsilon -closure( {2}) = C
\
\delta(D,0) = {6,9}
\
\epsilon -closure( {6,9}) = B
\
\delta(D,1) = \varnothing $$

所以可以得到DFA如下：

(3) Reduce the result of (2) and get a reduced DFA. 最终约简的DFA如下：

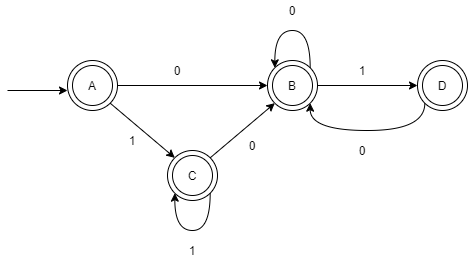
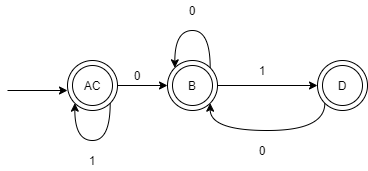
Exercise 3.5

Given the alphabet $\Sigma = { z, o, / }$ , a comment in a program over $\Sigma$ begins with “/o” and ends with “o/“. Embedded comments are not permitted.

(1) Draw a DFA that recognizes nothing but all the comments in the source programs.

(2) Write a single regular expression that exactly describes all the comments in the source programs.

(1) 做出的DFA如下：

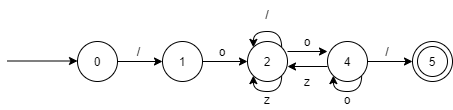
(2) 根据DFA可以写出如下的正则表达式：
$$
comments = /o (z \ | \ / \ | o \ o^* z)^* o^* o/
$$